나의 IT일지
힙 본문
하나의 노드에 여러개의 노드를 연결한 자료구조를 트리구조라고 하며, 트리구조중에서 주로 이진트리를 사용한다. 이진트리란 차수가 2개 이하로 구성되어 있는 트리구조로, 마지막 레벨을 제외하고 전부 채워저있는 완전이진트리와 완전이진트리에서 마지막 레벨을 모두 채운 포화이진트리가 이진트리에 속한다.

힙
완전 이진 트리에서도 부모 노드의 키 값이 자식의 노드의 키 값보다 항상 크거나 작은 형식을 가진 완전 이진 트리가 있는데, 이를 힙이라고 한다. 힙이란 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 완전 이진 트리로, 다음과 같은 조건을 가지고 있다.
- 완전 이진 트리여야 한다.
- 루트노드는 제일 크거나 작은 값을 가지고 있어야 한다.
- 형제간의 대소관계는 상관없이 모든 부모와 자식간의 대소관계는 명확헤야 한다.

위의 자료구조는 힙의 예시로, 루트노드는 제일 높은 값인 "14"를 저장하고 있으면, 루트 노드의 자식노드들은 루트노드 보다 작은 값인 "8, 13"을 저장하는 것을 확인 할 수 있다. 그리고 부모노드의 값인 "8, 13"에 대해서 자식노드의 값은 부모노드의 값보다 작은 "4, 7", "10, 12"가 저장되어 있다. 즉, 모든 자식노드의 키값이 부모노드의 키값을 넘지 않는 것을 확인 할 수 있다.
힙의 알고리즘
힙은 완전 이진트리이지만, 배열을 통해 힙의 노드에 있는 데이터 값을 저장한다. 그래서 노드의 구조체는 데이터만 저장하는 장소만 할당되며, 힙의 구조체도 배열형식으로 되어 있다.
typedef struct heapNodeType {
element data;
}heapNode;typedef struct heapType{
heapNode heap[MAX_ELEMENT];
int heap_size;
} heapType;즉, 힙은 리스트 형식으로 데이터를 저장하지만 이진트리의 형식으로 표현을 해야 한다. 그렇다면 힙은 어떻게 이진트리 형식으로 표현할까?
루트 노드의 값을 배열의 인덱스가 "1"인 노드에 저장하고, 한 단계 아래 요소를 왼쪽에서 오른쪽 순으로 배열에 저장하게 되면 다음과 같은 부모와 자식의 인덱스 관계가 형성 된다.
- 부모 노드 인덱스 = 자식 인덱스 / 2
- 왼쪽 자식 인덱스 = 부모노드 인덱스 * 2
- 오른쪽 자식 인덱스 = 부모 노드 인덱스 * 2 + 1

즉, 위의 그림처럼 힙의 데이터를 배열에 저장하면, a[i]의 부모 노드는 a[i/2], 왼쪽자식은 a[2i], 오른쪽 자식은 a[2i+1]인 부모와 자식의 인덱스 사이에서 관계가 형성된다.
- 힙 생성 함수
- 기능 : 힙을 표현할 배열리스트를 생성하며, 해당 배열의 정보(사용중인 요소 수) 저장
- 함수의 자료형: heapType의 포인터(heapType*)
| 알고리즘 |
| 1. 배열을 동적 메모리로 생성 후, 변수의 주소를 포인터 변수에 저장 2. 배열 정보 중 "heap_size"를 초기화 3. 리턴 값을 배열 정보를 가진 변수의 주소를 가진 포인터 변수로 지정 |
heapType* createHeap() {
heapType* h = (heapType*)malloc(sizeof(heapType));
h->heap_size = 0;
return h;
}
- 데이터 삽입 함수
- 기능
- 부모노드의 키값과 삽입할 데이터를 비교
- 부모노드의 키 값이 데이터보다 클 경우 : 해당 인덱스 자리에 데이터 삽입
- 부모노드의 키 값이 데이터 보다 작을 경우 : 해당 인덱스 자리에 부모노드의 키 값 삽입 후, 다음 부모노드와 의 키 값과 데이터 비교
- 2번 조건이 될 때 까지 3번 반복
- 함수의 자료형 : void
- 매개변수 : 데이터 삽입할 힙, 삽입할 데이터
- 필드 내의 변수 : i ← 데이터를 삽입할 인덱스 자리
- 기능

| 알고리즘 |
| 1. 사용중인 요소 변수의 값을 1 증가 2. i 에 사용중인 요소 변수의 값을 저장 3. 부모노드와 데이터 값 비교 (반복 시행) - 부모노드의 키 값이 삽입하려는 값보다 작은경우 : 부모노드의 값을 해당 인덱스에 저장한 뒤, i값을 다음 부모노드의 인덱스로 변경 -부모노드의 키 값이 삽입하려는 값보다 큰 경우 : 해당 인덱스에 데이터 값 저장 |
void insertHeap(heapType* h, int item) {
int i;
h->heap_size = h->heap_size + 1;
i = h->heap_size;
while ((i != 1) && (item > h->heap[i / 2].data)) {
h->heap[i].data = h->heap[i / 2].data;
i /= 2;
}
h->heap[i].data = item;
}
- 데이터 삭제 함수
- 기능
- 루트 노드에 있는 데이터 삭제
- 루트노드의 자식노드중 데이터 값이 큰 노드의 데이터 값을 루트 노드로 이동
- 이동하고 남은 노드를 기준으로 자식 노드중 데이터 값이 큰 노드의 데이터 값을 이동
- 이동하고 남은 노드의 자식 인덱스가 마지막 노드의 인덱스보다 작을 동안, 3번 반복
- 함수의 자료형 : 노드의 데이터의 자료형
- 매개변수 : 데이터를 삭제할 힙
- 필드 내의 변수
- parent ← 이동하고 남은 노드의 부모 인덱스, child ← 이동하고 남은 노드의 인덱스
- item ← 삭제할 데이터( 루트 노드의 데이터값), temp ← 마지막 인덱스의 데이터 값
- 기능

| 알고리즘 |
| 1. 마지막 인덱스를 제외해야 하기에 힙의 현재 사용중인 인덱스에서 "-1" 2. parent : 이동 노드의 인덱스, child : 이동 노드의 왼쪽 자식 노드의 인덱스 temp : 마지막 인덱스의 노드 데이터, item : 삭제하는 데이터 3. 데이터를 이동하는 노드의 인덱스의 범위가 현재 사용중인 인덱스의 범위 안에 있는 동안 1. 형제 노드간의 데이터 비교 후, 데이터가 큰쪽으로 child 변수가 이동 2. 데이터가 큰쪽의 형제 노드의 데이터와 마지막 인덱스의 노드의 데이터를 비교 - 마지막 인덱스의 노드가 큰 경우 : temp를 parent를 가진 노드에 저장 - 마지막 인덱스의 노드가 작은 경우 : parent를 가진 노드에 child를 가진 노드의 데이터 저장후, 다음 레벨로 이동후 반복 |
element deleteHeap(heapType* h) {
int parent, child;
int item, temp;
item = h->heap[1].data;
temp = h->heap[h->heap_size].data;
h->heap_size = h->heap_size - 1;
parent = 1;
child = 2;
while (child <= h->heap_size) {
if ((child < h->heap_size) && (h->heap[child].data) < h->heap[child + 1].data){
child++;
}
if (temp >= h->heap[child].data) {
break;
}
else {
h->heap[parent] = h->heap[child];
parent = child;
child = child * 2;
}
}
h->heap[parent].data = temp;
return item;
}
- 데이터 출력 함수
- 기능 : 힙에 저장되어 있는 데이터 출력
| 알고리즘 | 힙에서 사용되는 인덱스의 양만큼 반복해서 해당 노드에 있는 데이터 출력 |
void printHeap(heapType* h) {
int i;
printf("Heap : ");
for (i = 1; i <= h->heap_size; i++)
printf("[%d] ", h->heap[i].data);
}
데이터 삽입, 데이터 삭제, 데이터 출력하는 함수를 구현했으며, 해당 함수들을 통해 힙을 생성하면 다음과 같다.
#include <stdio.h>
#include <stdlib.h>
#define MAX_ELEMENT 100
typedef int element;
typedef struct heapNodeType {
element data;
}heapNode;
typedef struct heapType{
heapNode heap[MAX_ELEMENT];
int heap_size;
} heapType;
heapType* createHeap() {
heapType* h = (heapType*)malloc(sizeof(heapType));
h->heap_size = 0;
return h;
}
void insertHeap(heapType* h, int item) {
int i;
h->heap_size = h->heap_size + 1;
i = h->heap_size;
while ((i != 1) && (item > h->heap[i / 2].data)) { //부모노드의 키 값이 삽입하려는 값보다 작은경우
h->heap[i].data = h->heap[i / 2].data; // 부모노드와 대입하려고 한 자리의 값을 서로 바꿈
i /= 2; // 다음 부모노드와 비교하기 위함
}
h->heap[i].data = item;
}
element deleteHeap(heapType* h) {
int parent, child; //데이터 재배치하는 노드의 부모 인덱스, 데이터 재배치하는 노드의 인덱스
int item, temp; //삭제할 데이터, 마지막 인덱스의 노드의 데이터 저장 변수
item = h->heap[1].data;
temp = h->heap[h->heap_size].data;
h->heap_size = h->heap_size - 1;
parent = 1;
child = 2;
while (child <= h->heap_size) { //데이터 옮길 노드의 인덱스가 마지막 노드의 인덱스 범위 내에 있는가
if ((child < h->heap_size) && (h->heap[child].data) < h->heap[child + 1].data){ //형제 노드간의 데이터 크기 비교 => 큰쪽으로 이동
child++;
}
if (temp >= h->heap[child].data) { // 데이터가 큰쪽의 형제 노드의 데이터와 마지막 인덱스의 노드의 데이터를 비교 (마지막 인덱스의 노드가 큰 경우)
break;
}
else { //마지막 인덱스의 노드가 작을 경우
h->heap[parent] = h->heap[child];
parent = child;
child = child * 2;
}
}
h->heap[parent].data = temp;
return item;
}
void printHeap(heapType* h) {
int i;
printf("Heap : ");
for (i = 1; i <= h->heap_size; i++)
printf("[%d] ", h->heap[i].data);
}
int main(void) {
int i, n, item;
heapType* heap = createHeap();
insertHeap(heap, 10);
insertHeap(heap, 45);
insertHeap(heap, 19);
insertHeap(heap, 11);
insertHeap(heap, 96);
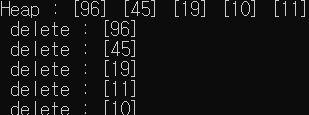
printHeap(heap);
n = heap->heap_size;
for (i = 1; i <= n; i++) {
item = deleteHeap(heap);
printf("\n delete : [%d] ", item);
}
// getchar();
return 0;
}