그래프

 자료구조는 1:1 구조인 선형구조와 1:n구조인 비선형구조로 구분되어 있다. 그런데 비선형 구조에서 여러 노드가 같은 노드를 가리키는 자료구조가 있는데, 이를 그래프라고 한다. 그래프란 n:n구조인 비선형구조로,  선형자료구조나 트리구조로 표현할 수 없다.

 그래프에서 데이터를 저장하는 노드를 정점(Vertex)이라고 하며, 정점과 정점을 연결한 선을 간선(Edge)라도 하며, 해당 그래프는 G=(V,E)로 표현한다.

 

그래프의 종류

무방향 그래프와 방향 그래프

• 무방향 그래프

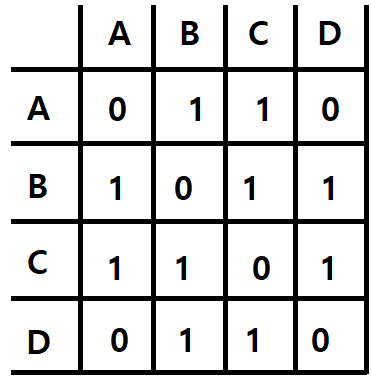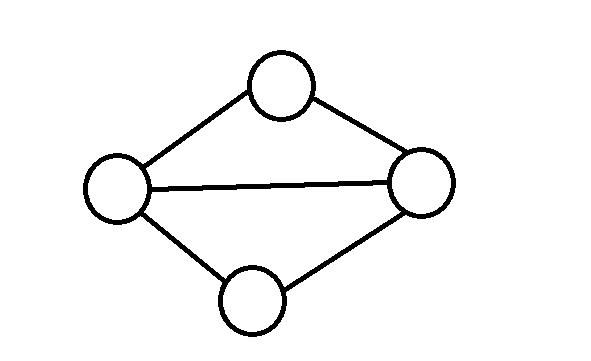
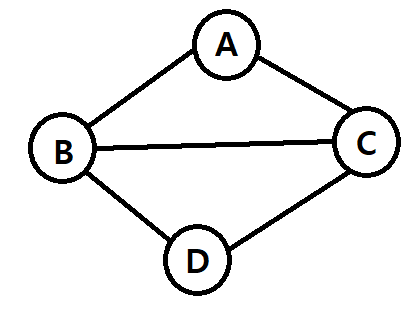
무방향 그래프 예시	인접 행렬

 정점과 정점을 연결한 간선의 방향이 없는 그래프로, 해당 간선을 통해 쌍방으로 이동이 가능하다. 이때, 해당 그래프의 정점들은 "V(G)"에 표현하며, 정점을 연결한 간선들은 연결된 정점들을 "(정점, 정점)"를 통해 "E(G)"에 표현한다.

 즉 해당 그래프의 정점은 "V(G) = { A, B, C, D }"으로 표현하며, 간선은 "E(G) = { (A,B), (A,C), (B,C), (B,D), (C,D) }로 표현한다.

 

• 방향그래프

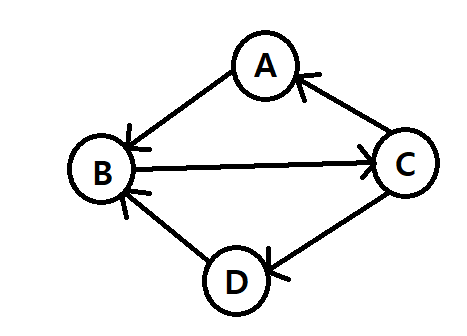
방향 그래프 예시	인접 행렬

 정점과 정점을 연결한 간선의 방향이 있는 그래프로, 해당 간선을 통해 한 방향으로 이동이 가능하다. 이때, 해당 그래프의 정점들은 "V(G)"에 표현하며, 정점을 연결한 간선들은 연결된 정점들을 "<출발 정점, 도착 정점>"를 통해 "E(G)"에 표현한다.

 즉 해당 그래프의 정점은 "V(G) = { A, B, C, D }"으로 표현하며, 간선은 "E(G) = { <A,B>, <C,A>, <B,C>, <D,B>, <C,D> }로 표현한다.

차수

그래프에서 두 정점을 연결해서 간선을 이룬다고 했을 때, 이 두 정점은 인접한다고 하며, 두 정점을 연결하는 간선은 정점에 부속되었다고 한다. 이때, 정점에 부속된 간선의 수를 차수라고 하는데, 무방향 그래프에서는 차수를 구분하지 않지만, 방향 그래프에서는 차수를 진입차수와 진출차수로 나뉜다. - 진입 차수 : 해당 정점으로 들어오는 차수 - 진출 차수 : 해당 정점에서 나가는 차수

 

완전 그래프와 부분 그래프

• 완전 그래프

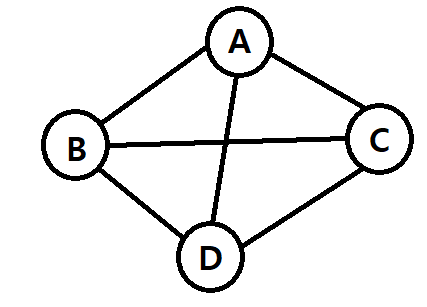
 모든 정점이 연결되어 있는 그래프로, 해당 완전 그래프가 가지는 간선의 수는 "정점*(정점-1)/2"이 된다. 즉, 위의 그래프는 간선이 6개인 정점이 4개 짜리 완전그래프인 것이다.

 

• 부분 그래프

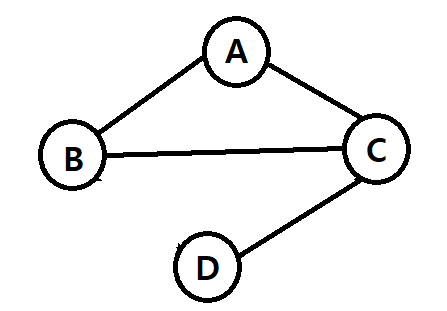
 원본 그래프에서 일정 부분의 정점이나 간선을 제외하고 만든 그래프로, 위의 그래프는 무방향 그래프에 있는 그래프의 부분그래프이며, 완전그래프의 부분그래프이다.

 

연결 그래프와 단절 그래프

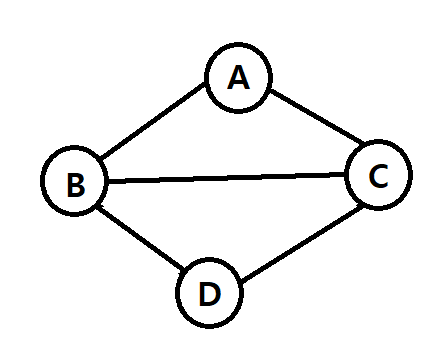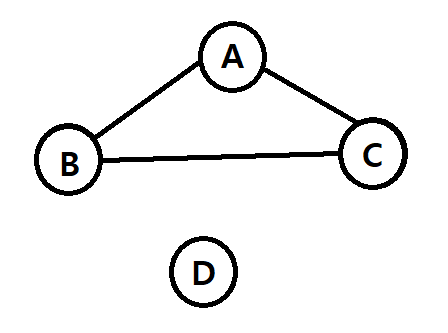연결 그래프	단절 그래프

 그래프는 정점과 정점이 간선으로 이어져 있으면 이를 연결되어 있다고 하며, 어떠한 간선이 이어져 있지 않는 정점이 있는 경우 이를 단절되어 있다고 한다. 즉 모든 정점이 간선으로 이어져 있는 그래프를 연결 그래프라고 하며, 하나의 간선이라도 이어져있지 않은 그래프 를 단절 그래프라고 한다.