트리 순회

 트리란 1:n구조로 하나의 노드에 여러개의 노드를 연결한 자료구조로, 노드와 노드를 연결한 선을 간선, 간선의 위쪽 노드를 부모노드, 간선의 아래쪽 노드를 자식노드라고 한다.

 그리고 부모노드가 갖는 자식노드의 숫자에 따라 차수가 결정이 되는데, 데이터를 검색하기 위해서는 이진 트리를 사용한다. 이때, 이진 트리는 차수가 2이하인 트리구조로, 왼쪽 자식과 오른쪽 자식을 구분한다.

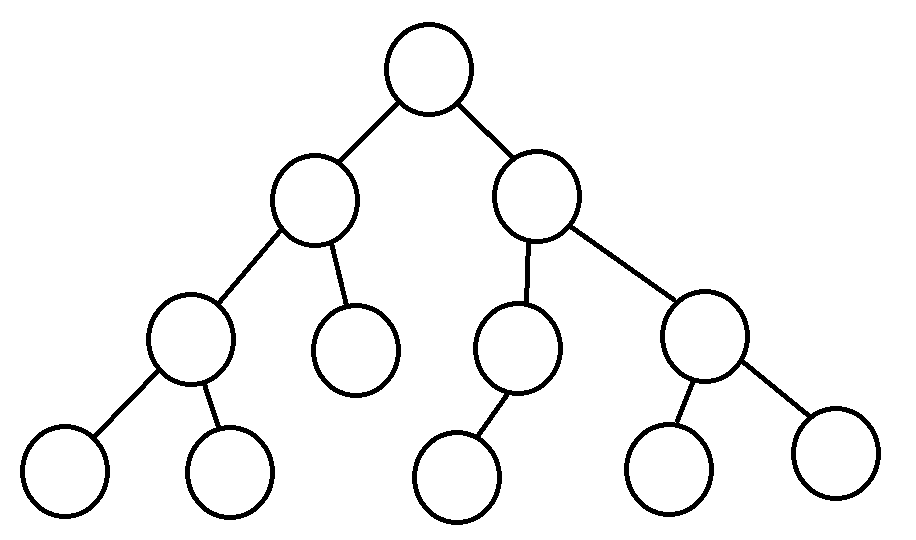
 그래서 이진 트리의 노드에는 데이터를 저장하는 필드와 오른쪽 노드와 왼쪽노드를 저장할 수 있는 필드가 필요하다.

typedef struct TreeNodeType {
	element data; //데이터 필드
	struct TreeNodeType* right; //오른쪽 서브트리
	struct TreeNodeType* left;  //왼쪽 서브트리
}treeNode;

 

트리 순회 방법

 트리의 노드에 저장되어 있는 데이터를 검색하기 위해서는 어떤 노드를 기준으로 모든 노드를 순회해야 한다. 이를 트리 순회라고 하는데, 트리 순회는 이진트리를 사용해야 하며, 왼쪽 서브트리, 왼쪽 노드를 먼저 순회한다.

 트리 순회에는 전위순회, 중위순회, 후위순회가 있으며, 노드를 순회를 위해 지나가는 것이랑 해당 노드의 데이터를 검색하는 것이랑 다르다.

• 전위 순회 : 부모노드 → 왼쪽 자식노드 → 오른쪽 자식노드

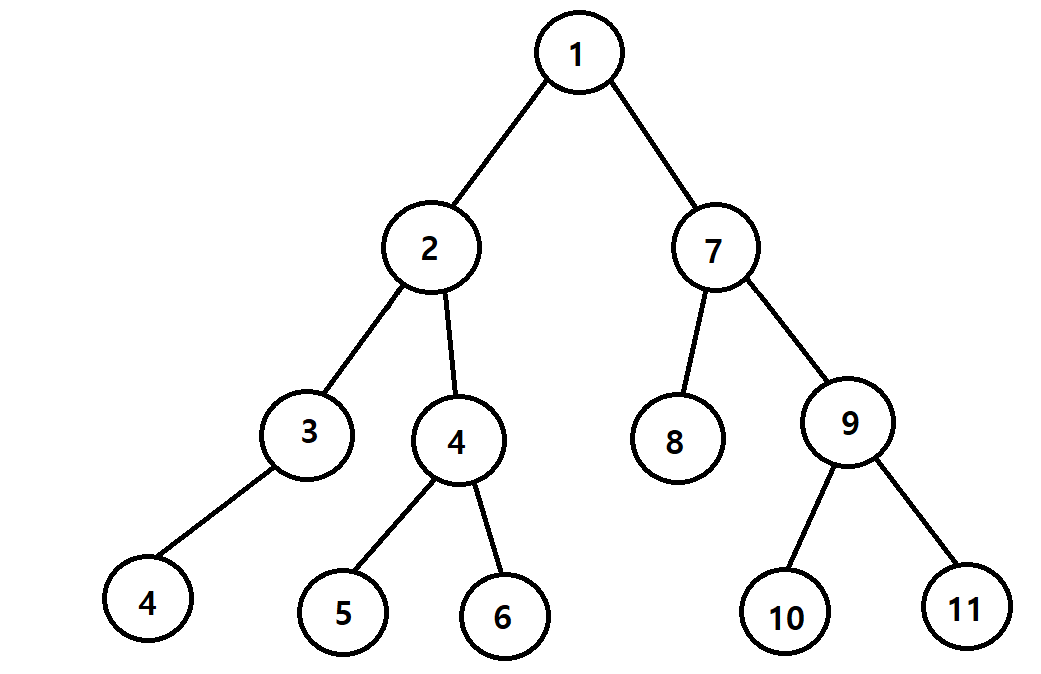
 전위 순회는 부모노드에 있는 데이터를 먼저 출력한 후, 왼쪽 노드, 오른쪽 노드순으로 출력한다. 

 2레벨이상의 이진트리에서는 루트노드를 기준으로 왼쪽 서브트리를 위의 방식으로 순회한 뒤, 오른쪽 서브트리를 위의 방식으로 순회한다. 즉 아래의 그림처럼 순회한다.

void preorder(TreeNode* root) {
	if (root) {
		printf("%c", root->data); //D
		preorder(root->LNode); //L
		preorder(root->RNode); //R
	}
}

 

• 중위 순회 : 왼쪽 자식노드 → 부모노드 → 오른쪽 자식노드

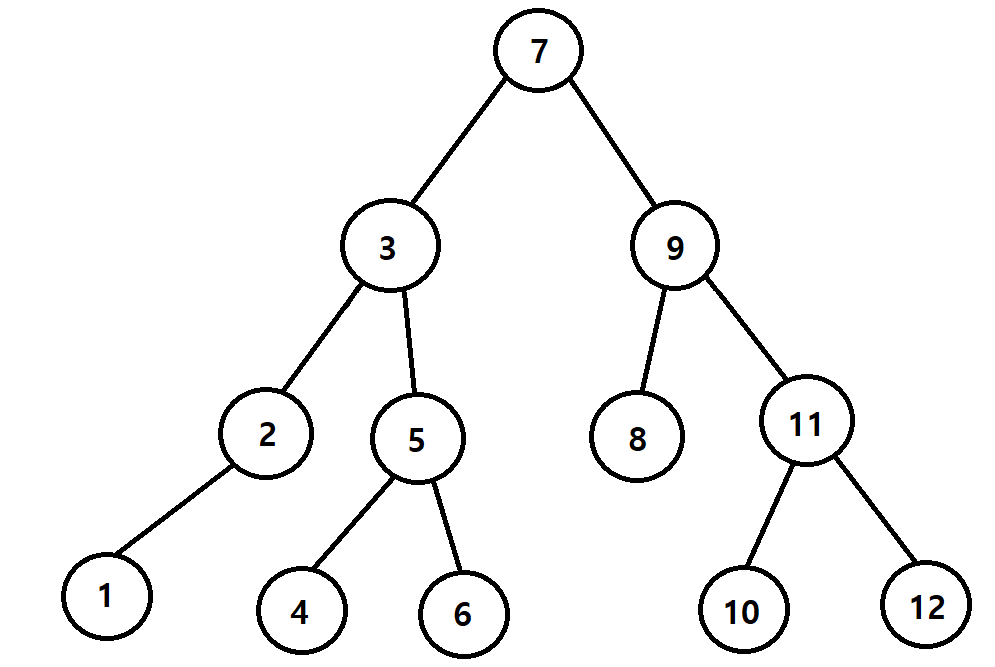
 중위 순회는 제일 왼쪽 노드에 있는 데이터를 먼저 출력한 후, 부모노드, 오른쪽 노드순으로 출력한다. 

 2레벨이상의 이진트리에서는 루트노드를 기준으로 왼쪽 서브트리를 위의 방식으로 순회한 뒤, 오른쪽 서브트리를 위의 방식으로 순회한다. 즉 아래의 그림처럼 순회한다.

void inorder(TreeNode* root) {
	if (root) {
		inorder(root->LNode);
		printf("%c", root->data);
		inorder(root->RNode);
	}
}

 

• 후위 순회 : 왼쪽 자식노드  → 오른쪽 자식노드 → 부모노드

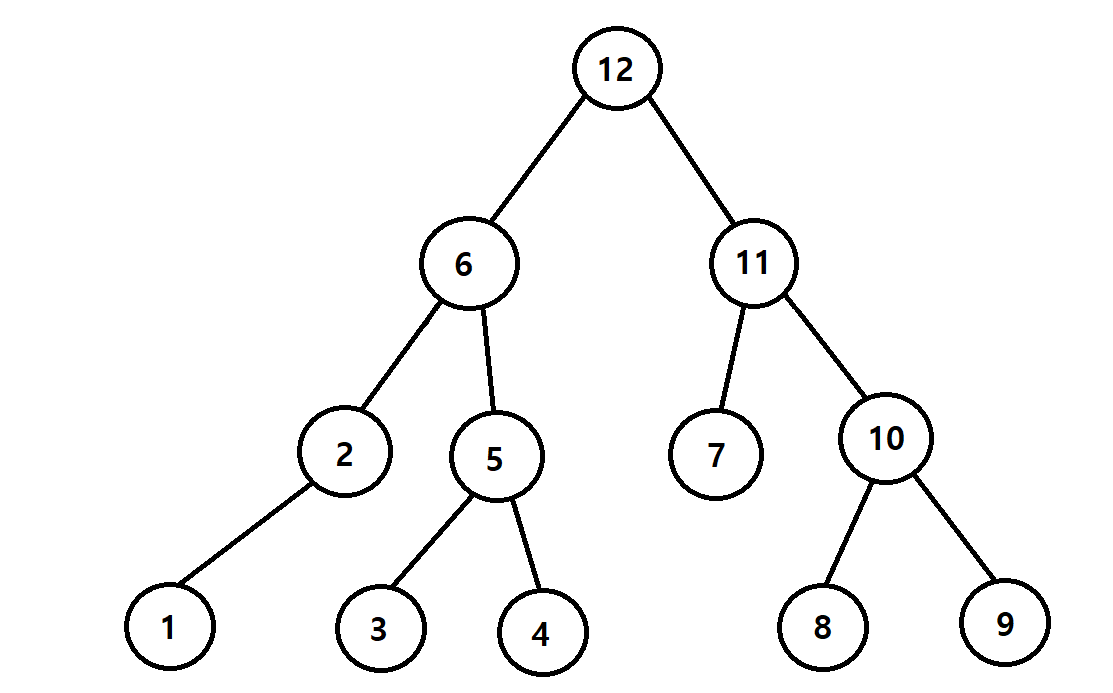
 후위 순회는 제일 왼쪽 노드에 있는 데이터를 먼저 출력한 후, 오른쪽 노드, 부모노드 순으로 출력한다. 

 2레벨이상의 이진트리에서는 루트노드를 기준으로 왼쪽 서브트리를 위의 방식으로 순회한 뒤, 오른쪽 서브트리를 위의 방식으로 순회한다. 즉 아래의 그림처럼 순회한다.

void postorder(TreeNode* root) {
	if (root) {
		postorder(root->LNode);
		postorder(root->RNode);
		printf("%c", root->data);
	}
}

 위의 순회 방법을 바탕으로 아래의 트리를 순회하면 다음과 같이 출력된다.

 

#include<stdio.h>
#include<stdlib.h>

typedef int element;

typedef struct TreeNodeType {
	element data;
	struct TreeNodeType* RNode;
	struct TreeNodeType* LNode;
}TreeNode;

TreeNode* makeNode(element data, TreeNode* L, TreeNode* R) {
	TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
	root->data = data;

	root->LNode = L;
	root->RNode = R;

	return root;
}

//전위 순회
void preorder(TreeNode* root) {
	if (root) {
		printf("%c", root->data); //D
		preorder(root->LNode); //L
		preorder(root->RNode); //R
	}
}

//중위 순회
void inorder(TreeNode* root) {
	if (root) {
		inorder(root->LNode);
		printf("%c", root->data);
		inorder(root->RNode);
	}
}

//후위 순회
void postorder(TreeNode* root) {
	if (root) {
		postorder(root->LNode);
		postorder(root->RNode);
		printf("%c", root->data);
	}
}

int main(void) {

	TreeNode* n7 = makeNode('G', NULL, NULL);
	TreeNode* n6 = makeNode('F', NULL, NULL);
	TreeNode* n5 = makeNode('E', NULL, NULL);
	TreeNode* n4 = makeNode('D', NULL, NULL);
	TreeNode* n3 = makeNode('C', n6, n7);
	TreeNode* n2 = makeNode('B', n4, n5);
	TreeNode* n1 = makeNode('A', n2, n3);

	printf("\n preorder : ");
	preorder(n1);

	printf("\n inorder : ");
	inorder(n1);

	printf("\n postorder : ");
	postorder(n1);

	return 0;

}